The Effects of Lead Counter-Weights on Inertia in Grand Piano Keys

A brief discussion of inertia in piano keys, and an example of its practical application Introduction:

As a piano technician, I often hear comments like the following: “I like the way the piano sounds, but can you ‘lighten’ the action up a little?” This sounds like a simple question, but an action’s feeling of “heaviness” can actually be caused by a number of different things. The first consideration is always to make sure the action parts are cleaned and well regulated. Normal service procedures are often enough to rid the action of unwanted sluggishness, and enable it to play with the responsiveness that it was designed to have. However, if the action is properly serviced, and it still feels “heavy”, solutions are more difficult to come by – at times they are all but impossible, without re-designing the action.

In certain circumstances though, some improvements can be made without replacing parts. These improvements require a basic understanding of the two individual elements of what we commonly refer to as “touch-weight” – and how changing the parameters of one of these elements will necessarily alter the effect the other has on the way the action feels. These two elements are the piano key’s balance weight – which is a static measure of the amount of weight needed to balance a key at mid-stroke and its inertial properties, which can be defined as the key’s ability to accelerate with a given amount of force. [The acceleration of a piano key would be very difficult to measure; but, given enough information, it can be calculated to a usefull degree of accuracy. This process, which deals with the same subject being described here, but in more refined detail, will be the subject of a future article. For now, only general trends are considered.]

Inertia in grand piano actions

When a grand piano action is assembled, the combined leveraged weight of the hammer/shank assembly, along with that of the wippen assembly, is normally great enough that, in the absence of lead counter weights installed in the front half of the keys, the action feels too “heavy”. Because of this, lead counterweights are added to the front of the key to make the touch feel “lighter”. The standard measurements for this “touch-weight” are down-weight (d) – the least amount of weight added to the front of the key that will cause the key to drop to the point of let-off; up-weight (u) – the greatest amount of weight added to the front of the key that will allow the key to return to its rest position; and balance weight (b) – calculated as the average of u and d. All of these are used to establish what amounts to a static design parameter for the “touch-weight” of the keyboard.

Although 40 grams is a common balance weight in many grand pianos (give or take a few grams), the number of lead weights needed to achieve this balance can vary significantly. The effective weight of the wippen and hammer assemblies on the back half of the key is primarily determined by the geometric configuration of these parts with respect to their axes of rotation and the leverage ratio of the key itself. This weight is what determines the amount of lead needed to balance the key.

Inertia – in a piano action, the key’s dynamic quality – is the resistance of an object to changes in its state of motion. In straight-line motion, the relationship between the object’s mass and its inertia is given by the equation: F=ma, or, a=F/m. In other words, there is a linear inverse relationship between an object’s ability to accelerate under the influence of a given net force, and its mass – the greater the mass, the more sluggish the acceleration.

This relationship is somewhat more complex in rotational motion – the motion of all piano action parts. The rotational analogue to the above equation is t=Ia, or, a=t/I, where t (torque) is the product of force and the distance between the point where the force is being applied, and the axis of rotation; I (moment of inertia) is the product of an object’s mass and its distance from the axis of rotation squared, and a (angular acceleration) is the quotient of the object’s tangential acceleration and the distance between the applied force and the axis of rotation. So, restating the relationship between force and acceleration in terms of angular motion: There is an exponential inverse relationship between an object’s ability to accelerate under the influence of a given net torque, and its moment of inertia – the greater the moment of inertia, the more sluggish the acceleration.

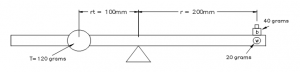
The diagram below is an abstract representation of these concepts applied to a piano key. T represents the combined leveraged weight of the hammer/shank assembly, along with that of the wippen assembly (or, top-weight), all acting on the back of the key at the capstan; w represents the lead counter weight in the front half of the key; b represents the balance weight at the front of the key.

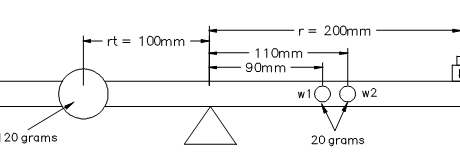
In figure 1, the lever is in static equilibrium – the clock-wise torque about the key’s balance point is equal to the counter clock-wise torque Tr_t = br + wr. When the balance weight is removed, the frictionless key would have a down-weight of 40g. The same is true in figure 2 – the opposing torques are balanced with a balance weight of 40g.

However, the dynamic properties of the two figures are different, and figure 2 will actually feel “lighter” when the two keys are played. Even though the combined mass of the counter weights in figure 2 (w₁ and w₂) is exactly twice that of the single mass in figure 1 (w), the combined moments of inertia of the two weights in figure 2 is less than that of the one weight in figure 1 – in this case .404gm² (gram meters²) and .8gm², respectively.

This simple concept shows that there is a range of inertial response to a given force at the front of the key that can be manipulated by the technician when rebuilding an action (this process could even be done at the end of a complete action regulation), and that range is determined by the placement of the lead counterweights with respect to the balance rail. This relationship can be summed up in the following statement: Within a given balance weight, the least amount of inertial resistance can be achieved by adding as much weight as possible, as close to the balance rail hole as possible, to achieve that balance weight; and the greatest amount of inertia is gained by doing the opposite: adding the least amount of weight, as far away from the balance rail hole as possible, to achieve the same balance weight.

Redistribution of counterweights

To demonstrate this concept, we re-weighed the keys on a piano that had recently had a new set of hammers installed. The existing pattern of lead counterweights was such that all of the weight was added as far out on the key (near the player’s finger) as possible, with a resulting balance weight that ranged from over sixty grams in the bass, to around 53 grams in the middle, slowly tapering to about 48 grams in the treble – and the leads numbered from three per key in the bass, two in the middle, and one or none in the treble. This, obviously, is a very high balance weight, and the action correspondingly felt quite heavy and difficult to control.

The first step involved adding lead to the keys to achieve an even balance weight of 42 grams from notes 1 thru 88. All added lead was installed as close to the balance rail as possible, minimizing the amount of added inertia. The result was not acceptable. Although the balance weight had been reduced significantly (by at least 10 grams in the middle of the piano) the action felt considerably “heavier”. While each key would begin to move with less force than before, the added inertia was obviously a problem.

To correct this, we removed one of the original lead weights from each key. This particular piano had originally been weighed off with every key (except the top octave) having one lead of 14 grams placed 70 millimeters from the front of the key. It was this lead that was removed from each key. The result brought the balance weight back up to where it originally was, but the keyboard felt noticeably “lighter” than it had to begin with, and a definite improvement had been made. The reason for this is that although the balance weight was the same as when we started, that balance weight had been achieved by shifting the lead counterweights closer to the balance rail, lowering the combined moments of inertia of each key’s balancing lead weights. In other words, the balance weight remained the same, but the dynamic properties had been improved.

There are, of course, practical limits to how much advantage can be gained in this way. For example, if there are already several leads in a key, and those leads are placed toward the front of the key (where the player’s finger rests), replacing those leads with weights near the balance rail might result in a situation where so much lead is needed, that there would hardly be room enough to insert the number of leads needed near the balance rail without placing at least some lead back in spots where lead had already been removed. In such a case, very little advantage could be gained, and the process would probably be a waste of time.

On the other hand, there may be cases when a piano’s action feels very heavy after inserting several leads in the keys to bring it to a balance weight of, say, 40 grams. Such an action may actually be made to feel “lighter” by simply removing some lead weights, thereby increasing the balance weight. (Actually, this process describes the effect of the final step of the above description, as compared to the unsatisfactory condition reached after the first step.) In any case, it should be clear that altering one aspect of touch-weight necessarily has an effect on the other; and as is the case with virtually everything else in piano service, a proper balance of various elements is needed to achieve the best results.

Copyright ©Joe Swenson 2011

All rights reserved

Other useful piano technical information by Joe Swenson.